About contributions to molecular orbitals

Frequently, it is useful for many applications to estimate populations of atomic orbitals followed by estimating the populations of atoms and molecular fragments.
However it may be done exactly only in the case when atomic orbitals are orthogonal to each other.
Generally it is not the case. However there are several methods to do it approximately.
Chemissian implements two schemes referred to as "Simple" and "Mulliken":

Molecular orbital is a linear combination of basis functions:

 
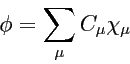
Simple contribution
The simplest way to estimate the contribution of atomic orbital into the given molecular orbital is to use the following expression:

 

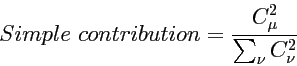
Mulliken contribution
In somewhat more "accurate" Mulliken scheme of population estimating atomic orbital contribution is calculated as follows:
 

 
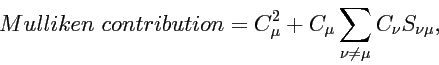
where is the overlap integral between the atomic orbitals and .

Summing contributions from individual atomic orbitals to molecular orbitals can give:

• Atomic contributions to molecular orbitals.
• Contribution of basis functions of a given angular momentum for each atom to MO
• Contribution of basis functions of a given shell for each atom to MO
• Molecular fragments contribution to MOs
• etc.